Konsep Denavit-Hartenberg

Manipulator mekanik terdiri dari sejumlah bagian tubuh yang dinamakan link dan joint. Joint digunakan untuk menghubungkan setiap link-link yang ada. Setiap joint mewakili satu derajat kebebasan. Untuk mendeskripsikan hubungan translasional dan rotasional antara link-link yang berdekatan digunakanlah konsep Denavit dan Hartenberg sebagai sebuah metode matriks yang secara sistematis membangun sebuah sistem koordinat dari masing-masing link.

Berdasarkan Andreas Bischo et al(1999.p20-21) Dalam mencari sebuah transformasi dari sebuah ujung alat hingga basis dari sebuah manipulator, ditentukan frame dari link-link dan mendapatkan teknik yang sistematikal, yang dapat menjabarkan kinematika dari sebuah robot dengan n derajat kebebasan dalam cara yang unik.

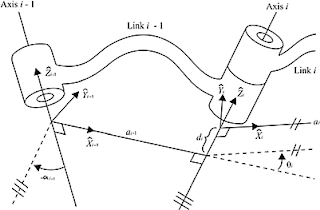
Notasi ini mendeskripsikan parameter hubungan antara satu sendi/lengan dengan sendi/lengan yang lain, Guna memodelkan lengan robot berjenis articulated robot, digunakan notasi Denavit- Hartenberg. Notasi ini mendeskripsikan parameter hubungan antara satu sendi/lengan dengan sendi/lengan yang lain, terdiri dari 4 parameter (ai, αi, di, θi ). Notasi ini ditulis pada sistem koordinat XYZ. Gambar 1 menunjukkan notasi Denavit-Hartenberg yang digunakan dalam paper ini.

Gambar. Notasi Denavit-Hartenberg

ai = jarak dari Z i ke Z i+1 diukur sepanjang X i

αi = sudut antara Z i dan Z i+1 diukur seputar X i

di = jarak dari X i−1 ke X i diukur sepanjang Z i

θi = sudut antara X i−1 ke X i diukur seputar Z i
Dengan notasi tersebut, posisi sebuah sendi yang terdapat pada ujung akhir sebuah lengan dapat dihitung berdasarkan posisi sendi ujung awal lengan, sudut sendi, dan panjang lengan. Karena sebuah sendi menghubungkan antara sebuah lengan dengan lengan lainnya, maka posisi end effector, yang pada simulator ini dimodelkan dengan sebuah gripper, dapat ditentukan.

1.   Denavit-Hartenberg (D-H) digunakan untuk menggambarkan hubungan link dari robot dimana link diasumsikan berbentuk benda tegar (rigid body)

2.         Setiap link_i memiliki sebuah kerangka koordinat (KK_i).

3.         Setiap KK ditentukan berdasarkan kaidah [K.S. Fu et.al] :

a.         Arah sumbu Z_i berimpit dengan sumbu pergerakan dari joint i+1

b.        Arah sumbu X_i

·           Sejajar Z_i-1 X Z_i (Cross product).

·     Apabila Z_i-1 dan Z_i paralel, maka arah sumbu X_i sejajar dengan garis tegak lurus bersama antara Z _i-1 dengan Z_i.

c.         Sumbu Y_i-1 mengikuti aturan tangan kanan

d.        Titik pusat KK_i     

·           Pada titik potong antara sumbu Z _i-1 dengan Z_i di sumbu Z_i

·           Titik potong  garis tegak lurus bersama antara Z _i-1 dengan Z_i

Perhatikan sumbu Z adalah sumbu joint

4.         Terdapat 4 parameter :

LINK PARAMETER (Lokasi relatif   2 buah sumbu di dalam Ruang)

a.       a_i (link length); Jarak dari titik potong antara sumbu Z_i-1 dengan sumbu X_i menuju titik pusat KK_i sepanjang sumbu X_i (atau jarak terpendek antara sumbu Z_i-1 dengan sumbu Z_i )

b.        Jarak dari sumbu Z_i-1 ke sumbu  Z _i  sepanjang garis tegak lurus bersama (common perpendicular)

·           Common perpendicular adalah jarak terpendek dua buah garis dalam ruang.

·           Common perpendicular tidak selalu terletak di dalam link.

·           Jika sumbu Z_I-1 dan Sumbu Z_i berpotongan a_i = 0

·           Tidak didefinisikan untuk Joint Prismatic, a_i = 0

c.     α_i (link twist); Sudut dari sumbu Z_i-1 menuju sumbu Z_i terhadap sumbu X_i (menggunakan aturan tangan kanan)

Joint Parameter

a.       d_i (link offset); Jarak dari titik pusat KK i-1 menuju ke titik potong antara sumbu Z_i-1 dengan sumbu X_i sepanjang sumbu Z_i-1. Berupa variabel untuk untuk Prismatic joint.

b.    θ_i (joint angle); Sudut dari sumbu X_i-1 menuju sumbu X_i terhadap sumbu Z_i-1 (menggunakan aturan tangan kanan)

Setelah parameter (a, a, d, q) setiap link telah ditentukan, persamaan matriks homogen dapat dibangun untuk membentuk hubungan antar KK terdekat (adjacent), atau  hubungan KK i  dengan KK i-1, dimana i menyatakan link ke i, yang pada prinsipnya adalah membuat agar kedua KK koordinat tersebut berimpit, yaitu melalui urutan operasi

a.         Putar sebesar sudut q_i terhadap sumbu Z_i-1 agar sumbu X_i-1 dengan sumbu X_i sejajar/parallel

b.        Translasikan sejauh d_i sepanjang sumbu Z _i-1 agar sumbu X _i dan sumbu X_i-1  berimpit (coincidence)

c.         Translasikan sejauh a_i sepanjang sumbu X_i  agar kedua titik pusat berimpit

d.        Putar sebesar sudut a_i terhadap sumbu X_i agar kedua KK berimpit

1.       Untuk joint berputar a_i, a_i dan d_i adalah konstanta, q_i variabel memenuhi hubungan : ^i-1 A _i =  T_z,d T_z,q T_x,a T_x,a

2.      Bentuk Inverse

3.    Untuk joint prismatic a_i, a_i dan q_i adalah konstanta, d_i variabel memenuhi hubungan : ^i-1 A _i = T_z,q T_z,d T_x,a

4.      Bentuk Inverse

5.      Contoh Matrik Transformasi untuk Robot PUMA dimana semua jointnya berputar